Wie im Bild oben zu erkennen bezeichnet Pandemie eine Seuche, die sich über ganze Landstriche, Länder oder sogar weltweit ausbreitet; während eine Epidemie nur ein begrenztes Gebiet betrifft.
Grundsätzlich stellt sich bei Vorhersagen die Frage, ob sie – zumindest theoretisch – möglich sind oder nicht und von wie viele Einflussgrößen zu bedenken sind:
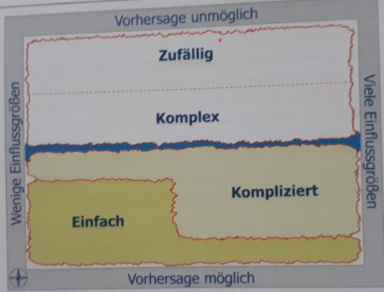
Das Bild zeigt eine „Landkarte“ mit einem „Fluss“. Oberhalb dieser Trennlinien wird die Vorhersage des Verhaltens zunehmend unmöglicher. (Erklärungen der Begriffe am Ende des Textes)
Beim Arbeiten mit Zahlen ist es natürlich (wie bei einer Textaufgabe in der Schule) wichtig, die richtigen Zahlen in die Rechnung einzutragen. Erfassung und Zählweisen von gesunden, infizierten, erkrankten, verstorbenen sind landes- wie weltweit nicht einheitlich geregelt, ebensowenig wie die Kriterien, nach denen getestet wird. Unterschiedliches Ausgangsmaterial an Zahlen bewirkt am Ende jedoch ganz unterschiedliche Ergebnisse und nachfolgend unterschiedliche Schlussfolgerungen!
Wissenschaftlich gesehen ist die Ebene der Expertenmeinung die schwächste Form der Validierung (Bestätigung einer Hypothese = Annahme). Auch wenn es die Einschätzung von Fachkundigen / Sachverständigen ist, die aufgrund ihrer Lebenserfahrung, ihres theoretischen Wissens oder der Erfahrungen aus spezialisierten Zentren eine Annahme vertreten, bleibt es am Ende eine Meinung und ist keine gesicherte Erkenntnis. Um herauszufinden, wie viele Menschen in Deutschland überhaupt infiziert sind, bräuchte es eine groß angelegte, repräsentative Bevölkerungsstichprobe. Erst mit testunabhängigen Studien kann berechnet werden, wie die Situation annähernd realistisch aussieht.
Die Annahmen bei dieser „Pandemie“ sind, a) die Infektion mit dem neuen Virus breite sich weltweit in gleicher Weise aus, unabhängig ob Stadt oder Land und b) das Virus sei hochtoxisch und die Entwicklung der Erkrankungen wird einen exponentiellen*) Verlauf nehmen.
*) Exponentiell heißt hier: ein Infizierter steckt mindestens zwei andere Menschen an und diese beiden stecken wiederum
zwei andere an, so dass sich eine Zahlenfolge von 1 – 2 – 4- 8 – 16 -32 -64 – 128 – 256 – usw. oder gar schneller ansteigend ergibt.
Beispiel: Verdoppelt man z.B. 1 Reiskorn 64 mal, wie es der Indische Kaiser Sheram dem Erfinder es Schachspiels zahlen wollte,
so ergibt das am Ende ca. 540 Milliarden Tonnen Reis. Das entspricht der Weltreisernte von ca. 870 Jahren.
Anfänglich bestätigt der Kurvenverlauf der weltweiten Infektionen eine solche Exponentialkurve (links); inzwischen, durch die staatlichen Maßnahmen, entwickelt sich der Verlauf jedoch anders (Kurve rechts).
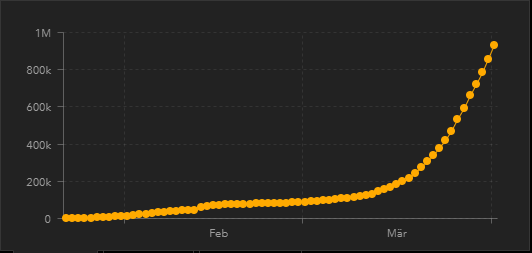
Coronarvirus Resource Center

In der Praxis steckt jedoch auch nicht jeder zwei weitere Menschen an, dafür aber ein anderer drei oder vier oder zu Beginn dieser Pandemie sogar im Mittel fünf bei irgendwelchen Großveranstaltungen.
Es läuft dann auf diesen schnellen exponentiellen Verlauf hinaus, wenn jeder Mensch im Mittel 2,73… andere ansteckt. Damit ist die Kontaktbegrenzung auf 2 Menschen zu erklären.
Jedoch erst wenn die mittlere Ansteckungsrate unter 1 fällt, steigt die Kurve nicht mehr an, die Neuerkrankungen werden weniger, die Epedemie läuft langsam aus – wenn es dabei bleibt!
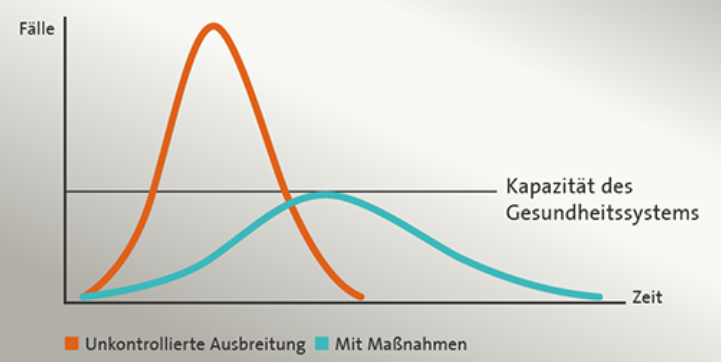
Die rote Kurve zeigt im aufsteigenden Schenkel einen exponentiellen Verlauf. Der Verlauf hat jedoch in einer begrenzten Welt ein natürliches Maximum – irgendwann gibt es niemanden mehr, den man noch anstecken könnte – und die Kurve fällt.
Die bislang, zur Vermeidung von Infektion, isoliert lebenden Menschen können wieder
– zumindest ohne diese spezielle Gefahr – in die Welt zurück.
Durch die Isolation und Vermeidung von Ansteckung, so hofft man, flacht der Kurvenverlauf ab (grüne Kurve).
Das wäre günstig, um die vorhandenen Möglichkeiten der medizinischen Versorgung weitgehend zu gewährleisten.
Allerdings geht dieses Szenario davon aus, dass die Menge der infizierten unter beiden Glockenkurven gleich ist.
Dabei geht man von einer Durchseuchung von ca. 70 % der Bevölkerung aus, bis die natürliche Grenze erreicht ist.
Vorstellbar ist jedoch auch, dass sich deutlich weniger Menschen infizieren und durch die Erkrankung mit körpereigenen Abwehrstoffen gegen das Virus immun werden. Ein weiterer Teil der Bevölkerung könnte, nach Entwicklung eines Impfstoffes, gegen die Erkrankung immunisiert werden. In diesem Fall könnte sich das gesellschaftliche Leben deutlich schneller normalisieren.
An einem einfachen Beispiel lässt sich ein komplexes Geschehen gut veranschaulichen:
Stellen wir uns ein gemütliches Naherholungsgebiet vor den Grenzen einer Stadt vor, ein kleiner See und ein netter Uferbereich. Es ist klar, dass dieses verlockende Fleckchen Erde im Sommer schnell überlaufen sein wird. Müll vom Picknick und Sonnencreme im Wasser bedeuten eine natürliche Grenze für das Ökosystem und seinen Erholungswert. Kommen also zu viele Städter, dann kippt das Ökosystem, der See fängt an zu stinken und aus ist es mit der Erholung.
Doch sobald der Sommer beginnt, fängt immer das gleiche Spiel an. Die ersten entdecken den kleinen See und erzählen ihren Freundinnen und Bekannten von den wunderbaren Erholungsmöglichkeiten. Aber je mehr kommen, desto mehr wenden sich auch wieder ab und sind enttäuscht vom überlaufenden Strand und dem zunehmende dreckigen Wasser und Wiesen..
Übersetzt: Am Anfang einer Infektionswelle kommt es zu immer mehr Infektionen (Die Besucher, also die Viren, „im See“ unseres Körpers breiten sich ungehindert aus), da man vor spürbaren Symptomen (größere Verschmutzung) ansteckend ist und die Freunde benachrichtigt, um mit ihnen den schönen Platz oder die Party dort gemeinsam zu genießen. Um der Entwicklung mit vielen, auch schwer erkrankten Menschen entgegenzuwirken, spricht die Regierung eine Kontaktsperre aus (z.B. Badeverbot am See).
Je mehr Leute sich daran halten, um so geringer die Infektionsmöglichkeiten (Verschmutzung des Sees und Geländes), die Zahl der Infizierten (Seebesucher) nimmt ab. Damit wäre die Gefahr gebannt, dass unser Gesundheitssystem von einem Ansturm der schwer Erkrankten überschwemmt wird und die Zahl der Betten und der Pflegekräfte die Zahl der Patienten übersteigt. (Das Naherholungsgebiet wäre gerettet.) … bis zum nächsten Mal!
Im Verlauf wird sich also irgendwann ein „Gleichgewicht“ einstellen, da alle Systeme nach solch einer „Homöostase“ streben, wo ihre Bewegung zur Ruhe kommen würde.
So wird es auch bei der Corona-Krise sein.
Dabei findet dieses Streben nach Gleichgewicht jenseits von unseren Moralvorstellungen oder von wünschenswerten Zuständen statt: eine neue Norm stellt sich einfach bei irgendeinem Punkt ein – egal ob einem das so gefällt oder nicht … und am Ende dieser vielen Zwischenschritte und Zwischengleichgewichte kommt das System zur Ruhe und ist zu Ende, tot bzw. geht in einen anderen Aggregatzustand über … bis schließlich alle Energie verbraucht ist und der ganze Prozess erstarrt.
Entsprechend wird auch nach der Corona-Krise ein neuer gesellschaftlicher Zustand gefunden werden müssen. Dies schon deshalb, weil einige Mitspieler verstorben sein werden, andere haben wirtschaftlich nicht überlebt und auch die Erkenntnisse dieser Erfahrung bleiben. Zum Teil bleiben auch Gesetze aus dieser Zeit erhalten und führen zu Veränderungen und nicht zuletzt müssen die entstandenen Kosten auch von irgendjemandem erarbeitet, bezahlt und verteilt werden. Da braucht es viele neue Antworten.
Man darf gespannt sein, welche Kräfte sich durchsetzen werden: Vernunft, Kooperation, Voraussicht und Daseinsfürsorge oder der Versuch eines „weiter so“, der dann später und auf Kosten der nachfolgenden Generationen zu schmerzlichem Nachsehen führen wird. Da kommt es darauf an, ob wir egoistisch denken „nach mir die Sindflut, ich hab´ nur ein Leben“ oder ob wir perspektivisch „unseren Kindern und Enkeln eine Welt hinterlassen, die ähnlich lebenswert ist, wie die unsere – zumindest in unseren Breitengraden.“
Auch bei den Ausstiegsszenarien müssen die Entscheidungsträger, trotz dünner Datenlage mit vermuteten Trends arbeiten. Das geschah bislang unter anderem mit der sogenannten Verdopplungszeit der gemessenen Neuinfektionen. Die Berechnung scheint einfach, die Bedeutung der Zahl simpel: je höher die Zahl, desto besser. Doch mathematisch wird die Verdopplungszeit unter der Annahme berechnet, dass die Zahl der infizierten exponentielle wächst. Das ist aber, aufgrund der bestehenden Einschränkungen, nicht mehr der Fall. Damit verliert die Zahl ihre Aussagekraft für Zukunftsprognosen.
Auch die Reproduktionsrate, die mit Hilfe einer App berechnet werden soll, sagt zwar aus, wie viele Menschen ein Infizierter im Duchschnitt ansteckt – je niedriger der Wert, desto besser -, doch einmal ist die Berechnung dieser Zahl komplex und zum anderen hängt sie daran, wie viele Menschen sich die App herunterladen und ihre Bewegungen offen legen. Je nachdem können die Wissenschaftler hierbei verschiedene Methoden anwenden, müssen dabei aber verschiedene Parameter abschätzen. Einmal bring diese Schätzung Unsicherheiten, zum anderen erbringen verschiedene Methoden unterschiedliche Ergebnisse. Der Mathematiker Prof. Dr. Moritz Kaßmann von der Uni Bielefeld empfiehlt daher, die Entwicklung ganz simpel an der Zahl der täglichen Neuinfektionen zu orientieren. Sinkt die Zahl über mehrere Tage, kann man das als positiven Trend verstehen.
Am Ende können alle Vorhersagen nur so gut sein, wie die Zahlen, aus denen sie berechnet wurden.
Quellen; Johns Hopkins University & Medicine, Coronarvirus Resource Center; Bundesgesundheitsministerium;
Systemische Praxis: Therapeutisches Chaos, Strunk und Schiepek, Hogrefe Verlag,
Gießener Anzeiger, 14. April 2020
Begriffserklärungen:
Einfach meint ein Verhalten, dass nur von wenigen Einflussgrößen hervorgebracht wird und völlig in ihrer Wenn-Dann-Relation verstanden werden kann.
Kompliziert beschreibt ein als problematisch bewertetes Verhalten das von vielen Einflussgrößen mitbestimmt wird, die prinzipiell bekannt und in ihrer Beziehung zueinander im Sinne von Gesetzmäßigkeiten verstanden werden kann.
Von Zufall sprechen wir, wenn die Mittel, ein Verhalten vorherzusagen, vollständig fehlen; z.B. wenn kein Zusammenhang zwischen den Ereignissen besteht. Dennoch lässt sich mit Mitteln der Stochastik und der Wahrscheinlichkeitsrechnung etwas über zufällige Prozesse sagen und zeigen, dass manche Ereignisse wahrscheinlicher sind als andere. Statistische Wahrscheinlichkeiten helfen aber für Aussagen zum Einzelfall nichts. Man kann sich da also nur allgemein auf etwas einstellen.
Komplexes (chaotisches) Verhalten sieht ähnlich aus, ist aber nicht mit Zufall zu verwechseln. Hier spielt die Zahl der Einflussgrößen keine wesentliche Rolle. Dennoch werden, wie beim Zufall, die Vorhersagen über das Verhalten eines Systems schnell so schlecht, wie beim Wetterbericht: dort ist schon nach 3 Tagen die mögliche Variation der Entwicklungen so groß, dass Aussagen reine Raterei sind. Dennoch gestaltet sich das Verhalten der Einflussgrößen auf wissenschaftlich beschreibbaren Regeln. Ein System ist nämlich nichts anderes als Elemente und deren Beziehungen untereinander. Dabei ist die Annahme, dass das alles irgendwann verstanden werden kann, irreführen.)